TopCoder SRM 587 - 900: ThreeColorability

Problem Statement

给出一个 n*m 的方格，每个方格还要连一条对角线，对角线的形状分为"N"形和"Z"形，就是主对角线和副对角线。
现给你一个这样的图，有的正方形对角线连法已经确定，有的没确定，
问你是否能把图补完整，使其顶点可以被3-染色。
若可以，返回一组字典序最小的解(NZ形成的二维字符串)。
1 <= n,m <= 50

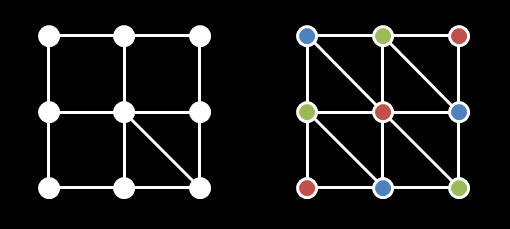
There is a H times W rectangle divided into unit cells. The rows of cells are numbered 0 to H-1 from top to bottom, and the columns are numbered 0 to W-1 from left to right. The corners of cells are called lattice points. By definition, there are (H+1)*(W+1) lattice points in our rectangle.

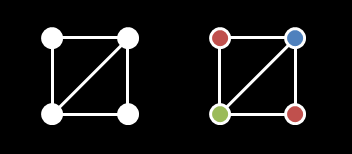
Each of the four edges of each cell is painted white. Additionally, in some cells exactly one of the two diagonals is painted white. In the remaining cells no diagonal is painted white yet. Later, you are going to paint exactly one of the diagonals white in each of these cells.

Once you are done painting the diagonals, your next goal will be to color each of the lattice points using one of three available colors: red, green, or blue. There is only one constraint: adjacent lattice points are not allowed to share the same color.

Two lattice points are called adjacent if they are connected by a white line segment. (In other words, consecutive corners of a cell are always adjacent, opposite corners of a cell are adjacent if and only if they are connected by a painted diagonal, and no other pairs of lattice points are adjacent.)

Obviously, you need to paint the missing diagonals in such a way that there will be a valid coloring of lattice points, if possible.

You are given a String[] cells with H elements, each consisting of W characters. If cells[i][j] is 'N', there is a diagonal line from the top left to the bottom right corner in the cell in row i, column j. If cells[i][j] is 'Z', there is a diagonal line from the top right to the bottom left corner in the cell in row i, column j. If cells[i][j] is '?', there is no diagonal yet in the cell in row i, column j.

If it is impossible to fill in the missing diagonals in such a way that there will be a valid coloring of all lattice points, return an empty String[]. Otherwise, return a String[] that represents the rectangle with all the missing diagonals filled in. I.e., the return value must be obtained from cells by replacing each '?' by either 'N' or 'Z'. The return value must represent a rectangle for which a valid coloring of its lattice points exists. If there are multiple possibilities, return the lexicographically smallest one.

Definition

Class ThreeColorability
Method lexSmallest
Parameters vector<string>
Returns vector<string>
Method signature vector<string> lexSmallest(vector<string> cells)

(be sure your method is public)

Limits

Time limit (s) 2.000
Memory limit (MB) 64

Notes

Given two different String[]s A and B with the same number of elements, find the smallest index i such that A[i] and B[i] differ. If A[i] < B[i] we say that A is lexicographically smaller than B and vice versa.

Constraints

cells will contain between 1 and 50 elements, inclusive.
Each element of cells will contain between 1 and 50 characters, inclusive.
All elements of cells will contain the same number of characters.
Each character of cells will be either 'N' or 'Z' or '?'.

Test cases

input
- cells { "Z" }
output
Returns { "Z" }

note

The given rectangle and a possible coloring is as follows.
input
- cells {"??",
  "?N"}
output
Returns {"NN",
"NN"}

note
input
- cells {"ZZZ",
  "ZNZ"}
output
Returns { }
input
- cells {"N?N??NN",
  "??ZN??Z",
  "NN???Z?",
  "ZZZ?Z??",
  "Z???NN?",
  "N?????N",
  "ZZ?N?NN"}
output
Returns { }
input
- cells {"ZZZZ",
  "ZZZZ",
  "ZZZZ"}
output
Returns {"ZZZZ",
"ZZZZ",
"ZZZZ"}

back to the menu